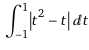>>1353136Step 1: check the conditions of the curve without absolute values.
Differentiate it, say how many minimums and maximums it has and where.
It's function of 2nd order, it had only one minimum/maximum. Now you know where the curve goes up and where down. (2t-1=0 : t=0.5)
Do second derivative to know the curvature in this point (2= local minimum)
Now check the y values for the left side of the interval and the right one. Find the point where it is zero and is located within the interval.
Left side at -1 has value of 2
Right side has value of 0.
It cuts the X axis in spots 0 and 1
Now you know that curves y value starts at 2, goes down till 0, crosses the axis here, at 0.5 it goes up and crosses the y axis at 1.
So all values from left till 0 are positive, all values between 0 and 1 are negative.
Absolute of positive is positive
Absolute of negative is positive times minus one
This means you do integral from -1 to 0 of f(t) plus integral from 0 to 1 of -f(t)= -t^2+t